培养探索精神，促进深度教学

——《钉子板上的多边形》教学实践与思考

江阴市临港实验学校  吴萍

 

【摘要】 《钉子板上的多边形》是苏教版教材安排的一次规律的探索活动。大多数教师都会沿着教材给定的素材和探索的方法指导学生研究，从而得出结论。这其实是一种被动的接受学习，忽视了对素材的甄别、策略的自主生成能力的培养，课堂仅仅停留在浅层次的“找规律”。而我们在教学中，除了关注“探索什么”、更加注重“用什么探索”和“怎样探索”，真正达到探索规律的育人价值。

【关键词】素材  策略  角度  延展

 

《钉子板上的多边形》是一次研究平面图形面积的数学活动。学生参与这样的数学活动既有趣味性，同时又极具挑战性。因为此次活动要探索围成的图形面积与图形的边上和图形的内部钉子枚数之间的关系，还要用含有字母的式子准确的表达这种关系，有相当的思维挑战性。纵观教材，探索活动主要分三段来进行：围成的图形内部只有1枚钉子时的规律；围成的图形内部有2枚钉子时的规律；围成的图形内部有3枚、4枚钉子或没有钉子时的规律。在实际教学中，我们是沿着教材给定的素材和策略，从单一的角度，引导学生“找到”规律呢？还是深层次地发掘，引导学生自主地“探究”规律。下面，笔者就结合教学实践，从以下几个方面和大家探讨。

一、素材的呈现

“探索”一般是指应用多种方法寻求答案的过程。作为数学学科的过程性目标，探索的目的不仅包括寻求解决问题的思路，发现事物的特征及一般规律，也包括培养学生探寻未知事物的一种精神。教学中，我们要将学生置身于一个原生态的、真实问题情境之中，还原科学探索的本来面目，经历探索过程的艰难和挫折，这样才能让学生真正体会探索的成功和喜悦。

【片段1】

师：课前，老师让同学们用橡皮筋在钉子板上围了很多不同的多边形（出示图1）。在钉子板上横行和竖行中每相邻的两枚钉子之间是1厘米。你能看图算出每个多边形的面积吗？

 

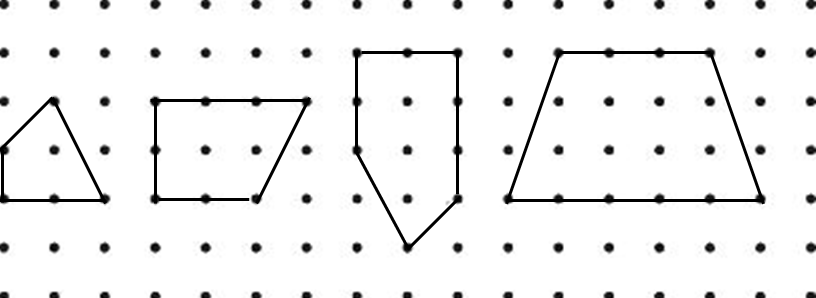
学生看图逐个数出或者算出每个多边形的面积并交流反馈。

师：请同学们大胆地猜想一下，钉子板上多边形的面积可能与什么有关？

生1：我认为可能与钉子数有关。

师：与哪里的钉子数有关？

生2：我认为与多边形内部的钉子数有关。

生3：我觉得与围成多边形的边上的钉子数有关。

生4：可能与内部的钉子数和边上的钉子数都有关系。

师：多边形的面积和钉子数是否有关？如果有关，有怎样的关系？下面我们就借助同学们课前围好的多边形进行研究。

出示表格，让学生数一数、算一算，填写表格，然后组织交流反馈。

图形编号	多边形的面积（平方厘米）	边上钉子数	内部钉子数
①
②
③
④

师：观察思考，多边形的面积与边上的钉子和内部的钉子有关吗？如果有关，他们之间存在怎样的关系？先自己独立思考，再在小组内交流。

学生在组内充分交流的基础上进行全班交流。

生1：我们组觉得内部的钉子数越多，多边形的面积就越大；边上的钉子数越多，面积也越大。

生2：我们组也是这样想的，但是它们之间的变化好像没有什么规律。

生3：我们组发现边上的钉子数是单数，那么多边形的面积就是小数；如果边上的钉子数是双数，则多边形的面积就是整数。

生4：我们组认为钉子板上多边形的面积和边上的钉子数、内部的钉子数肯定有什么规律，我们觉得可以再围一些多边形找一找。

从以上的教学片段可以看出，当学生猜测多边形的面积可能与内部的钉子数和边上的钉子数有关后，教师并没有直接出示学生一眼就能找到规律的内部只有1枚钉子的图形，而是呈现了学生课前围成的内部钉子数不同的图形。学生在进行苦苦思考之后，他们发现边上的钉子数、内部钉子数都在变化，多边形的面积与它们好像没有什么规律。但是直觉告诉他们钉子板上多边形的面积与钉子数有关，所以还产生了“再围一些多边形”的想法。学生在经历初次探索失败后，他们学会对自己猜想的质疑，产生了对素材的甄别需要，也为后续探索策略的选择埋下伏笔。

 二、策略的选择

探索的过程是一种积极的学习过程。在实际的课堂教学中，是让学生经历探索策略的形成过程，还是沿着教师给定的策略直接得到结论？是让学生指向对策略的自主筛选，还是指向策略的直接应用？很显然，前者更能体现学生的主体地位，也更体现了数学的育人价值。

【片段2】

师：同学们通过观察和思考能到了很多有价值的问题。下面我们重新回到开始时的几个图形，思考一下，多边形的面积可能受到几个数量的影响？

生1：多边形的面积可能受内部钉子数的影响。

生2：多边形的面积也受到边上钉子数的影响。

师：是的，我们在研究多边形面积和边上钉子数的规律时候，内部的钉子数在变；在研究多边形面积和内部钉子数的规律时候，边上的钉子数在变，这样的变化使我们不容易找到其中的规律。美国的数学家舍费尔德有这样的一段话（课件出示）：固定其他因素，只让一个量变化，从而得到问题的结果。

师：你是怎样理解这句话的？这句话又给你什么启发？

生1：就是让其中一个数量固定不变，只让另一个数量变化。

生2：我们可以让内部的钉子数不变，研究边上的钉子数与多边形面积之间的关系。

生3：我们也可以让边上的钉子数不变，研究内部钉子数与多边形面积之间的关系。

师：如果固定内部的钉子数，你会从内部钉子数是几枚的情况研究呢？

生：1枚，因为这样比较简单。

师：好的，今天我们的研究就从内部是1枚钉子数的情况开始。想一想，刚才的几个图形我们要怎样调整？

生：要换成内部都是1枚钉子的图形。

教师呈现内部1枚钉子的一组图形，学生进一步进行规律的探索。

学生在经历初次探索的失败后，感悟到多边形的面积与边上的钉子数和内部的钉子数这两个数量有关，但不太容易发现其中的规律。教师在此基础上出示数学家舍费尔德的话，引导学生自发的思索探究的策略：要么固定内部的钉子数，要么固定边上的钉子数。接着引导学生思考：如果固定内部的钉子数要从几枚开始研究？明确从1枚开始研究最为简单易行。从上述的教学活动看出，探究规律的策略不是教师直接告知，而是在数学家理性的思想引领下自主生发的。这样的探究过程才更完整，更充分。

三、观察的角度

数学观察能为规律的探索提供更多的感性材料，以便进一步发现问题和分析问题。在实际观察过程中，我们不仅要帮助学生注意到一些显见的问题，更应拓展他们的思维，从容易被忽略的信息中提出自己独特的见解，培养他们的创新思维。

【片段3】

师：当内部钉子数为1枚，多边形的面积和边上的钉子数有什么关系？请大家想一想，算一算，并在作业纸的表格上填一填（如下图）。

图形编号	内部钉子数	边上钉子数	多边形的面积（平方厘米）
①	1	5	2.5
②	1	6	3
③	1	7	3.5
④	1	8	4

学生独立完成后进行交流和汇报，明确：当内部的钉子数是1时，多边形的面积等于边上的钉子数除以2。

师：如果用字母S表示多边形的面积，n表示边上的钉子数，a表示内部的钉子数，那么我们刚才的规律用字母怎样表示？

生：a＝1时，S=n÷2   

师：刚才我们是横向观察的，如果我们换一个角度纵向观察，你又有什么新的发现？

生：我发现边上的钉子数每次多1枚，那么多边形的面积就每次多0.5平方厘米。

师：这位同学变换观察的角度，为我们拓宽了思路，真棒！

课件出示内部是2枚钉子的一组图形和表格（如下图），请你数一数、填一填。

图形编号	内部钉子数	边上钉子数	多边形的面积（平方厘米）
①	2	5	3.5
②	2	6	4
③	2	7	4.5
④	2	8	5

师：与刚才的表格相比，有什么相同和不同的地方？

生：相同的地方是边上的钉子数没有变，不同的地方是内部的钉子数多1，多边形的面积也多1。

师：你发现多边形的面积和边上的钉子数有什么关系？

生：多边形的面积等于边上的钉子数除以2，再加上1。

师：用字母式字母表示？

生：当 a＝2时，S=n÷2+1

师：刚才我们是横向观察，如果纵向观察，你又有什么发现？

生1：边上的钉子数每次多1枚，那么多边形的面积就每次多0.5平方厘米。

生2：这和我们刚才发现内部是1枚的钉子的多边形的规律是一样的。

生3:也就是说，内部的钉子数不变，边上的钉子数每增加1枚，多边形的面积就会增加0.5平方厘米。

师：接着我们研究什么情况呢？

生：可以研究内部钉子数是2枚、3枚、4枚等等的规律。

……

纵观本节课的教学，大部分的教师都会引导学生比较同一个图形中边上的钉子数和多边形面积之间的关系，然后通过多个横向的观察，得出多边形面积的公式。然而我们在实际教学中并没有局限于此。在教学内部钉子数分别是1枚、2枚、3枚……，得出多边形的面积公式的同时，我们鼓励学生变换观察的角度，归纳出：“边上的钉子数不变，内部的钉子数多1，多边形的面积也多1”，“内部的钉子数不变，边上的钉子数每增加1枚，多边形的面积就会增加0.5平方厘米”等这样的结论。不同角度的观察，使学生深入思考，各抒己见，充分的体会到探索规律的乐趣，也培养了他们良好的观察品质。

四、规律的延展

数学知识之间本身都有着紧密联系。探索规律的教学是要让学生积累活动经验，学会数学的方法，发展他们的数学思维。在课堂总结的环节，一般教师都会提问：“回顾刚才的学习过程，你有什么收获？”，让学生对本节课的规律探索稍作概括。其实，课堂结尾处既是问题消失的地方，同时也是问题产生的地方。我们可以充分的挑起学生的好奇心，引发他们进一步深度地思考，实现课堂价值的最大化。

【片段4】

师：今天这节课我们探索的是什么规律？

生：钉子板上多边形的面积等于边上的钉子数除以2，加上内部的钉子数再减1。

师：其实，这就是奥地利数学家皮克发现的规律，叫做“皮克定理”。同学们也和数学家一样经历了规律探索的全过程。想一想，我们是怎样发现这个规律的？

生1：我们从最简单的情况开始研究，然后再研究复杂的情况。

生2：多边形的面积和钉子板内部的钉子数和边上的钉子数有关，我们固定内部的钉子数，研究边上的钉子数和面积的关系。

生3：我们通过观察和分析得到了猜想，然后再举出例子来验证我们的猜想。

生4：我们的观察可以有不同的角度，这样可以得到更多有趣的发现。

师：如果还有更多的时间，你还会展开哪些有关的研究？

生1：我会固定边上的钉子数，研究内部的钉子数和多边形的面积之间的关系。

生2：我会研究这个皮克定理可以应用在哪些方面？

生3:我会研究更多有关多边形面积的计算方法。

师：同学们，皮克定理中为什么要用“边上的钉子数除以2”？

生：因为内部的钉子数不变，边上的钉子数每增加1枚，多边形的面积就会增加0.5平方厘米。

师:那为什么还要加上内部的钉子数再减1呢？

生：……

在回顾和反思的环节，学生不仅反思了探究的策略、观察的方法等方面，还进一步思考，想研究“皮克定理的应用”、“固定边上的钉子数，研究内部钉子数和面积的关系”等问题。同时在最后教师也及时沟通皮克定理中“边上的钉子数除以2”和“边上增加1枚钉子，面积就增加0.5平方厘米”，“加上内部的钉子”和“内部增加1枚钉子，面积就增加1平方米”等的内在联系。这样的结尾，不仅留给学生对所学知识的沟通和回顾，也留给学生更多的反思和思考，同时又再次地激发学生探究的欲望，收到了更好的效果。

从“找”规律到“探索”规律，不仅需要让学生经历探索的过程，更要培养学生探索的精神和能力。需要教师真正的让学生站在课堂的正中央，经历探索素材的自主甄别、探索策略的自主生发，同时需要提高学生观察的品质，培养他们思维的深刻性和独特性，引发深度教学的应然生成，促使数学学习走向更高境界。

 

参考文献：

【1】张祖润.小学数学“探索规律”的意义、编排与教学策略[J].中小学教师培训，2017（10）

【2】沈重予，于曦晖.苏教版小学数学教材中的“探索规律”[J] .小学数学教育，2016（9）

 

 

附件：